马尔科夫链蒙特卡洛法

发表于 | 分类于
快速回顾马尔科夫链蒙特卡洛法的基本知识点~

概览

马尔科夫蒙特卡洛法(Markov Chain Monte Carlo, MCMC)经常用在贝叶斯概率模型的推理和学习中,主要是为了解决计算困难的问题。日常中我们会用采样的方法采集样本，进行近似的数值计算，比如计算样本均值，方差，期望。虽然许多常见的概率密度函数(t分布，均匀分布，正态分布..)，我们都可以直接在numpy, scikit-learn中找到，但很多时候，一些概率密度函数，特别是高维的概率密度函数，并不是常见的分布，这个时候我们就需要用到MCMC啦。 在开始马尔科夫蒙特卡洛法之前，我们先简单的介绍一些蒙特卡洛法和马尔科夫链。

蒙特卡洛法 Monte Carlo

蒙特卡洛法是比较宽泛的一系列算法的统称(你要想了解以这个赌场自行google)，它的特点是假设概率分布已知，通过重复的随机采样来获得数值结果。比如根据大数定理，我们可以用采样得到的样本计算得到的样本均值来估计总体期望(例子1)。又比如，积分的运算往往可以表示为随机变量在一个概率密度函数分布上的期望(例子2)。

例子1： 假设有随机变量$x$，定义域$X$，其概率密度函数为$p(x)$, f(x)为定义在$X$上的函数，目标是求函数$f(x)$关于密度函数$p(x)$的数学期望$E_{p(x)}[f(x)]$。 蒙特卡洛法根据概率分布$p(x)$独立地抽样$n$个样本$x_1,x_2,…..x_n$,得到近似的$f(x)$期望为:

\[E_{p(x)}[f(x)] \approx \frac{1}{n} \sum_{i=0}^n f(x_i)\]

例子2： 假设我们想要求解$h(x)$在$X$上的积分:

\[\int_{X}h(x)dx\]

我们将$h(x)$分解成一个函数$f(x)$和一个概率密度函数$p(x)$的乘积，进而又将问题转换为求解函数$f(x)$关于密度函数$p(x)$的数学期望$E_{p(x)}[f(x)]$:

\[\int_{X}h(x)dx = \int_{X} \frac{h(x)}{p(x)}p(x)dx = \int_{X}f(x)p(x)= E_{p(x)}[f(x)]\]

这里，$f(x)$表示为$\frac{h(x)}{p(x)}$，则有:

\[\int_{X}h(x)dx = E_{p(x)}[f(x)] \approx \frac{1}{n} \sum_{i=0}^n f(x_i)\]

更一般的，假设我们想要求解$\int_0^{10} x^2dx$，熟悉积分的同学肯定已经知道答案为$\frac{1000}{3}$ (hint: $\frac{1}{3}x^3$)，那么如何用采样的方法来得到这个值呢?

令 \(p(x)=\frac{1}{10} \quad 0< x < 10\), 那么 $f(x)=10 * x^2$

1
2
3
4
5
6
7
8
 
import random
numSamples = 10000
# 在 0-10的均匀分布内采样
samples = [random.uniform(0,10) for _ in range(num_samples)]
f_samples = [10 * sample ** 2 for sample in samples]
result = 1/10000.0 * sum(f_samples)
#>>> result
#333.7766822849899

对于复杂的$h(x)$, 这种方法计算起来显然就更加方便啦。(特别是忘记积分怎么算的同学 :speak_no_evil:)

到这里为止，我们简单的介绍了蒙特卡洛方法，但是依旧没有提到要怎么利用复杂的概率密度函数进行采样。接下来我们来看一下接受-拒绝法(accept-reject sampling method)，它也是蒙特卡洛法中的一种类型适用于不能直接抽样的情况。

接受-拒绝法

假设有一个非常复杂不常见的分布$p(x)$，我们没有现成的工具包可以调用后进行采样，那么我们可以用我们已经有的采样分布比如高斯分布作为建议分布(proposal distribution)，用$q(x)$表示，来进行采样，再按照一定的方法来拒绝当前的样本，使得最后得到的样本尽可能的逼近于$p(x)$。

首先我们需要找到一个常数$k$使得$kq(x)$一定大于等于$p(x)$, 也就是如图所示(图摘自[2])，$p(x)$在$q(x)$下面。接着对$q(x)$进行采样，假设得到的样本为$z_0$。然后我们按照均匀分布在$(0, kq(z_0))$中采样得到$u$。如果$u$落到了图中的灰色区域，则拒绝这次采样，否则接受样本$z_0$。重复这个过程得到一系列的样本$z_0,z_1,…z_n$。

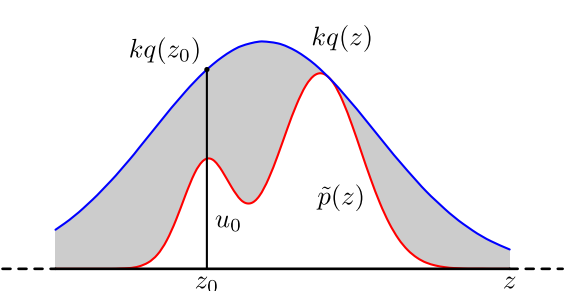
AcceptReject

在这个过程中，我们可以发现只有当建议分布$q(x)$和复杂分布$p(x)$重合的尽可能多的地方的样本更有可能被接受。那么相反的，如果他们重合部分非常少，那么就会导致拒绝的比例很高，抽样的效率就降低了。很多时候我们时候在高维空间进行采样，所以即使$p(x)$和$q(x)$很接近，两者的差异也可能很大。

我们可以发现接受-拒绝法需要我们提出一个建议分布和常量，而且采样的效率也不高，那么我们就需要一个更一般的方法，就是我们的马尔科夫蒙特卡洛法啦。不过MCMC依旧有个问题, 它的抽样样本不是独立的。到了Gibbs Sampling的部分，我们可以看到它做了一些小trick，来假装使得样本独立。

马尔科夫链

马尔科夫链的定义和概念相信大家都很熟悉了(不熟悉的请google)。在这里，我们回顾一下几个重要的知识点:

平稳分布

平稳分布 设有马尔科夫链 $X={X_0, X_1, …, X_t, …}$, 其状态空间为 $S$, 转移概率矩阵为 $P=(p_{ij})$, 如果存在状态空间$S$上的一个分布

\[\pi= \begin{bmatrix} \pi_1 \\ \pi_2 \\\vdots \end{bmatrix}\]

使得 $\pi=P\pi$

则称$\pi$为马尔科夫链$X={X_0, X_1, …, X_t, …}$的平稳分布

我们可以理解为，当一个初始分布为该马尔科夫链的平稳分布的时候，接下来的任何转移操作之后的结果分布依然是这个平稳分布。注意，马尔科夫链可能存在唯一平稳分布，无穷多个平稳分布，或者不存在平稳分布。

其它定理:

  1. 不可约且非周期的有限状态马尔科夫链，有唯一平稳分布存在。

  2. 不可约、非周期且正常返的马尔科夫链，有唯一平稳分布存在。

其中，不可约和正常返大家请自行查阅相关定义。 直观上可以理解为，任何两个状态都是连通的，即从任意一个状态跳转到其它任意状态的概率值大于零。

遍历定理

遍历定理 设有马尔科夫链 $X={X_0, X_1, \dots, X_t, \dots }$, 其状态空间为 $S$, 若马尔科夫链$X$是不可约、非周期且正常返的，则该马尔科夫链有唯一平稳分布$ \pi= \begin{pmatrix} \pi_1, \pi_2, \dots \end{pmatrix}^T $, 且转移概率的极限分布是马尔科夫链的平稳分布。

\[\lim_{t \to +\infty} P(X_t=i|X_0=j)=\pi_i \quad i=1,2,\dots; j=1,2,\dots\]

直观上,$P$最后会收敛成这个样子:

\[\lim_{t \to +\infty} P^n= \begin{pmatrix} \pi_1 & \pi_1 & \dots & \pi_1 & \dots \\ \pi_2 & \pi_2 & \dots & \pi_2 & \dots \\ \dots & \dots & \dots & \dots & \dots \\ \pi_j & \pi_j & \dots & \pi_j & \dots \\ \dots & \dots & \dots & \dots & \dots \end{pmatrix}\]

注意: 这里的$P_{ij}$表示的是第j个状态转移到第i个状态的概率。也就是说每一列表示这个状态转移到其它状态的概率。 我们可以理解为，当时间趋于无穷时，马尔科夫链的状态分布趋近于平稳分布。 另外，无论初始的分布$\pi’$是什么，经过了$n$次转移后, 即$P^n\pi’$, 最后都会收敛到它的平稳分布$\pi$ (原理待补充)。结合这两点，我们就可以用马尔科夫链进行采样。

首先我们随机一个样本$x_0$，基于条件概率(转移概率)$P(x|x_0)$ 采样$x_1$，因为我们需要转移一定次数后才会收敛到我们的平稳分布，所以比如我们设定了m次迭代后为平稳分布，那么 $(x_m, x_{m+1}, \dots)$ 即为平稳分布对应的样本集。

但是，要怎么确定平稳分布$\pi$(我们希望采样的复杂分布)的马尔科夫链状态转移矩阵或者转移核$P$呢？ 在开始MCMC采样之前我们还需要回顾两个知识点: 可逆马尔科夫链和平衡细致方程。

可逆马尔科夫链

可逆马尔科夫链 设有马尔科夫链 $X={X_0, X_1, \dots, X_t, \dots }$, 其状态空间为 $S$, 转移概率矩阵为$P$, 如果有状态分布$\pi= \begin{pmatrix} \pi_1, \pi_2, \dots \end{pmatrix}^T$，对于任意状态$i,j \in S$, 对于任意一个时刻$t$满足:

\[P(X_t=i|X_{t-1}=j)\pi_j=P(X_{t-1}=j|X_t=i)\pi_i, \quad i,j=1,2, \dots\]

或简写为:

\[p_{ji}\pi_j = p_{ij}\pi_i, \quad i,j=1,2, \dots\]

该式也被称之为细致平衡方程。

定理: 满足细致平衡方程的状态分布$\pi$就是该马尔科夫链的平稳分布。即 $P\pi = \pi$

因此，可逆马尔科夫链一定有唯一平稳分布，所以可逆马尔科夫链满足遍历定理的条件。

马尔科夫链蒙特卡洛法

我们先来看一下MCMC方法的大致思路: 在随机变量$x$的状态空间$S$上定义一个满足遍历定理的马尔科夫链$X={X_0, X_1, \dots, X_t, \dots }$, 使其平稳分布就是抽样的目标分布$p(x)$。然后在这个马尔科夫链上进行随机游走，每个时刻得到一个样本。根据遍历定理，当时间趋向于无穷时，样本的分布趋近于平稳分布，样本的函数均值趋近函数的数学期望。 读者可能会和笔者刚读到这段话的时候也有些疑惑，1. 如何定义这个能满足条件的马尔科夫链呢? 2. 这里的随机游走(转移核)采样具体是怎么实现的?

对于第一个问题，定义满足条件的马尔科夫链，大家也许猜到了可以用可逆马尔科夫链的性质定义一些特殊的转移核来保证遍历定理成立。但是我们又该如何保证这个特殊的转移核最后可以走到我们期望采样的复杂分布$P(x)$呢？看起来还是一头雾水。我们接着往下看。

Metropolis-Hastings

Metropilis-Hastings 算法是马尔科夫链蒙特卡洛法的代表算法。假设要抽样的终极概率分布是$p(x)$,它采用的转移核为:

\[p(x,x') = q(x,x')\alpha(x, x')\]

其中$q(x,x’)是另一个卡尔科夫链的转移核，并且是一个容易抽样的分布，被称之为建议分布。而$\alpha(x, x’)$ 被称为接受分布:

\[\alpha(x,x') = min\{1, \frac{p(x')q(x',x)}{p(x)q(x,x')} \}\]

到这里为止，读者可能觉得好像又和之前的拒绝-接受法很相似了呢。但是不同的地方是之前我们在拒绝-接受法里需要定义的建议分布还是比较难设定的，因为它需要满足一定的条件才可以。但是这里的建议分布相是一个比较容易抽样的分布。同理，我们根据建议分布$q(x,x’)$来进行随机游走，产生样本后，按照接受分布$\alpha(x, x’)$ 来确定是否要进行转移。那接下来，我们需要解决的主要问题是，如何证明通过这个方式最后生成的样本是符合$p(x)$分布的呢? 也就是说，如何证明这个转移核 $p(x,x’)$ 满足遍历定理以及最后的平稳分布是$p(x)$呢?

证明略。:laughing: 其实我们只要能证明这个构造出来的转移核$p(x,x’)$对应的马尔科夫链是可逆的，并且其对应的平稳分布就是$\pi$即可。也就是说需要证明:

\[p(x)p(x,x')=p(x')p(x',x)\]

证明:

\[\begin{align} p(x)p(x,x') &= p(x)q(x,x')min\{1, \frac{p(x')q(x',x)}{p(x)q(x,x')}\} \\ &=min\{p(x)q(x,x'),p(x')q(x',x)\} \\ &=p(x')q(x',x)min\{\frac{p(x)q(x,x')}{p(x')q(x',x)},1\}\\ &=p(x')p(x',x) \end{align}\]

并且根据细致平衡方程，$p(x)$即为这个转移核$p(x,x’)$的平衡分布。

在给出M-H方法的总体流程之前，我们先来看几个特殊的建议分布。

建议分布

对称建议分布

假设我们的建议分布是对称的，即$q(x,x’)=q(x’,x)$, 那么我们的接受分布$\alpha(x,x’)$ 可以写成:

\[\alpha(x,x')=min\{1, \frac{p(x')}{p(x)}\}\]

特别地, $q(x,x’)=q(|x-x’|)$ 被称为随机游走Metropolis算法, 例子:

\[q(x,x') \propto exp(-\frac{(x'-x)^2}{2})\]

读者也很容易发现，当正态分布的方差为常数，均值为$x$, 参数为$x’$的这些转移核都满足这种类型。这种类型的转移核的特点是，当$x’$在均值$x$附近的时候，其概率也就越高。

独立抽样

前面的抽样过程中，可以发现下一个样本总是依赖于前一个样本。那么我们假设设定的建议分布q(x,x’)与当前状态$x$无关，即$q(x,x’)=q(x’)$, 此时的接受分布$\alpha(x,x’)$ 可以写成:

\[\alpha(x,x') = min\{1, \frac{p(x')q(x)}{p(x)q(x')} \}\]

书上说，这样的抽样虽然简单，但是收敛速度慢，通常选择接近目标分布$p(x)$的分布作为建议分布$q(x)$。

接下来，我们看一下M-H方法的总体过程。

Metropolis-Hastings 算法步骤

输入: 任意选定的建议分布(状态转移核)$q$,抽样的目标分布密度函数p(x), 收敛步数m, 需要样本数n。

Step1. 随机选择一个初始值$x = x_0$, 样本集合 $samples=[]$

Step2. for t=0 to m+n:

  • 按照建议分布$q(x,x’)$ 随机抽取一个候选状态 $x’$

  • 计算接受概率:

    \[\alpha(x,x') = min \{1, \frac{p(x')q(x',x)}{p(x)q(x,x')} \}\]
  • 从区间$(0,1)$中按均匀分布随机抽取一个数$u$。若$u \le \alpha(x,x’)$，则状态$x=x’$ 否则，$x$保持不变
  • if (t >= m) 将$x$加入到samples中

Step3. 返回样本集合 $samples$

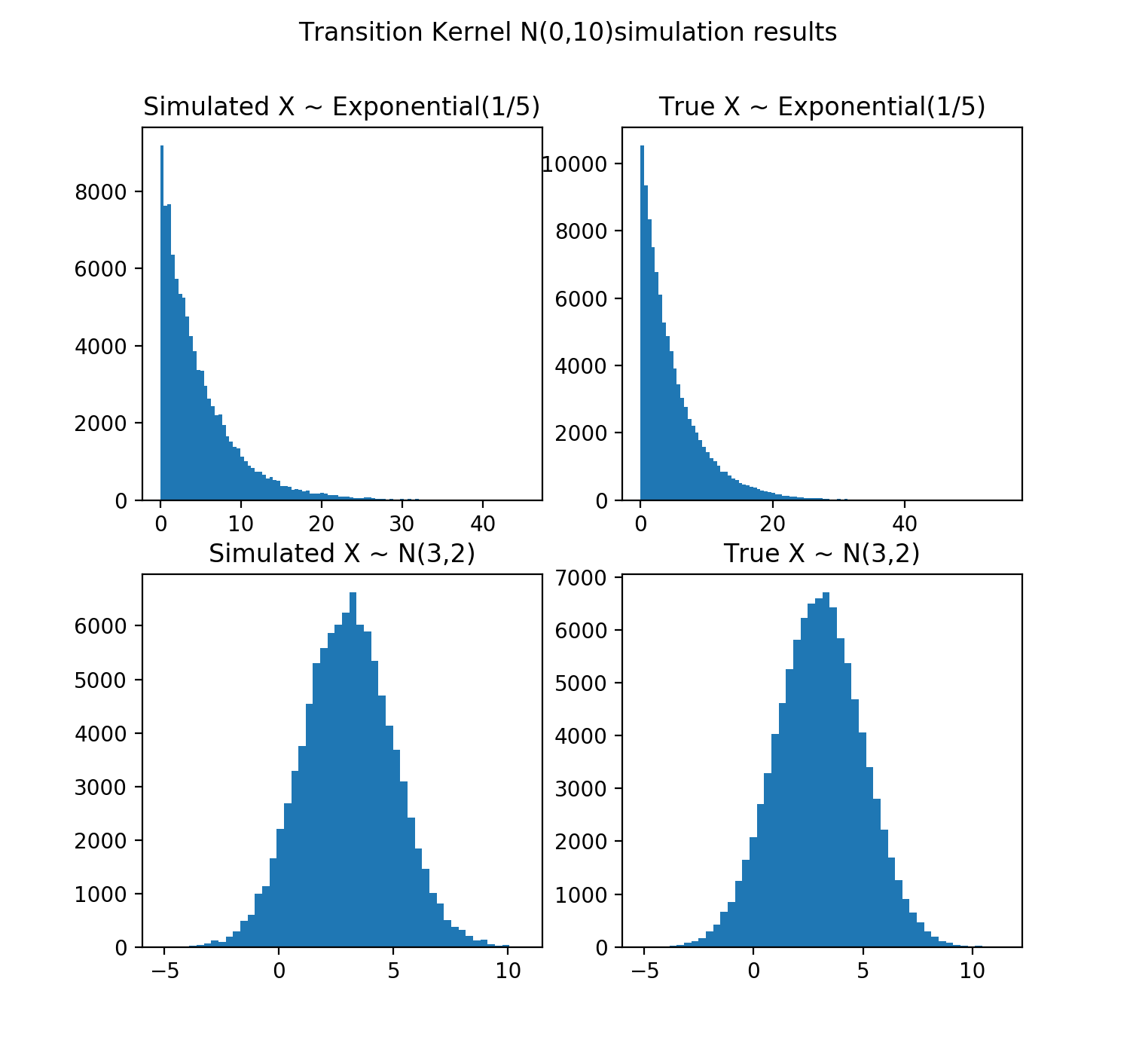
一个简单的例子:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
 
# -*- coding:utf-8 -*-

import random
import numpy as np
import matplotlib.pyplot as plt


def mh(q, p, m, n):
    # randomize a number
    x = random.uniform(0.1, 1)
    for t in range(0, m+n):
        x_sample = q.sample(x)
        try:
            accept_prob = min(1, p.prob(x_sample)*q.prob(x_sample, x)/(p.prob(x)*q.prob(x, x_sample)))
        except:
            accept_prob = 0

        u = random.uniform(0, 1)

        if u < accept_prob:
            x = x_sample

        if t >= m:
            yield x


class Exponential(object):
    def __init__(self, scale):
        self.scale = scale
        self.lam = 1.0 / scale

    def prob(self, x):
        if x <= 0:
            raise Exception("The sample shouldn't be less than zero")

        result = self.lam * np.exp(-x * self.lam)
        return result

    def sample(self, num):
        sample = np.random.exponential(self.scale, num)
        return sample


# 假设我们的目标概率密度函数p1(x)是指数概率密度函数
scale = 5
p1 = Exponential(scale)


class Norm():
    def __init__(self, mean, std):
        self.mean = mean
        self.sigma = std

    def prob(self, x):
        return np.exp(-(x - self.mean) ** 2 / (2 * self.sigma ** 2.0)) * 1.0 / (np.sqrt(2 * np.pi) * self.sigma)

    def sample(self, num):
        sample = np.random.normal(self.mean, self.sigma, size=num)
        return sample

# 假设我们的目标概率密度函数p1(x)是均值方差分别为3,2的正态分布
p2 = Norm(3, 2)


class Transition():
    def __init__(self, sigma):
        self.sigma = sigma

    def sample(self, cur_mean):
        cur_sample = np.random.normal(cur_mean, scale=self.sigma, size=1)[0]
        return cur_sample

    def prob(self, mean, x):
        return np.exp(-(x-mean)**2/(2*self.sigma**2.0)) * 1.0/(np.sqrt(2 * np.pi)*self.sigma)


# 假设我们的转移核方差为10的正态分布
q = Transition(10)

m = 100
n = 100000 # 采样个数

simulate_samples_p1 = [li for li in mh(q, p1, m, n)]

plt.subplot(2,2,1)
plt.hist(simulate_samples_p1, 100)
plt.title("Simulated X ~ Exponential(1/5)")

samples = p1.sample(n)
plt.subplot(2,2,2)
plt.hist(samples, 100)
plt.title("True X ~ Exponential(1/5)")

simulate_samples_p2 = [li for li in mh(q, p2, m, n)]
plt.subplot(2,2,3)
plt.hist(simulate_samples_p2, 50)
plt.title("Simulated X ~ N(3,2)")


samples = p2.sample(n)
plt.subplot(2,2,4)
plt.hist(samples, 50)
plt.title("True X ~ N(3,2)")

plt.suptitle("Transition Kernel N(0,10)simulation results")
plt.show()

代码运行结果: m_h_simulation

多元情况

在很多情况下，我们的目标分布是多元联合概率分布$p(x)=p(x_1, x_2, \dots, x_k)$, 我们可以用条件分布概率的比来计算联合概率的比，从而提升计算效率。即:

\[\frac{p(x'_I | x'_{-I})}{p(x_I |x_{-I})} = \frac{p(x')}{p(x)}\]

其中, $x_I={x_i, i \in I}, x_{-I}={x_i, i \notin I}, I \subset K={1,2, \dots, k}$，并且$p(x_I|x_{-I})$ 被称为满条件分布(full conditional distribution)。

而在用转移核对多元变量分布进行抽样的时候，可以对多元变量的每一个变量的条件分布一次分别进行抽样，从而实现对整个多元变量的一次抽样。

针对多元变量的情况，我们来讨论一下其中的一个特例，吉布斯采样(Gibbs Sampling)。

Gibbs Sampling

吉布斯采样(Gibbs Sampling) 适用于多元变量联合分布的抽样和估计。比较特殊的地方是它的建议分布是当前变量$x_j, j= 1,2,\dots,k$的满条件概率分布:

\[q(x,x')=p(x'_j|x_j)\]

这是，接受概率$\alpha=1$,

\[\begin{align} p(x)p(x,x') &= p(x)q(x,x')min\{1, \frac{p(x')q(x',x)}{p(x)q(x,x')}\} \\ &=min\{1, \frac{p(x'_{-j})p(x'_j|x'_{-j})p(x_j|x'_{-j})}{p(x_{-j})p(xj|x_{-j})p(x'_j|x_{-j})}\}\\ &=1 \end{align}\]

其中，$p(x_{-j})=p(x’_{-j})$ 因为不难想象, 假设对第$j$个变量采样前$x=(x_1, x_2, \dots, x_j, \dots, x_k)$， 对其采完样后$x’=(x_1, x_2, \dots, x’_j, \dots, x_k)$，那么在$x’$中分别去掉第 $j$ 项， 剩下的其余变量全部相同，所以它们的概率值也相同。

同理 $p(\cdot |x_{-j})=p(\cdot | x’_{-j})$

我们可以发现因为$\alpha$ 接受分布永远等于1，那么吉布斯采样是不会拒绝样本的。

(这里需要注意的是，这里的目标分布的单个元的分布至少应该是可以采样的，当然如果单个元很复杂的话，还是可以再用一次M-H的方法来为这个单元的分布进行采样。存疑)

吉布斯采样算法

输入: 抽样的目标分布密度函数$p(x)$, 转移核$q(x,x’)=p(x’_j|x_j)$ 收敛步数m, 需要样本数n。

Step1. 随机选择一个样本$x^{(0)}=(x_1^{(0)}, x_2^{(0)}, \dots, x_k^{(0)})$, 样本集合 $samples=[]$

Step2. for i=1 to m+n:

  • $x^{(i)}=x^{(i-1)}$

  • for j=1 to k:

    根据$p(x_j |x_1^{(i)}, …, x_{j-1}^{(i)}, x_{j+1}^{(i-1)}, \dots, x_k^{(i-1)})$ 抽取 ${x’}_j^{(i)}$, 并赋值给$x^{(i)}[j]$

  • if (i >= m) 将 $x^{(i)}$ 加入到samples中

Step3. 返回samples

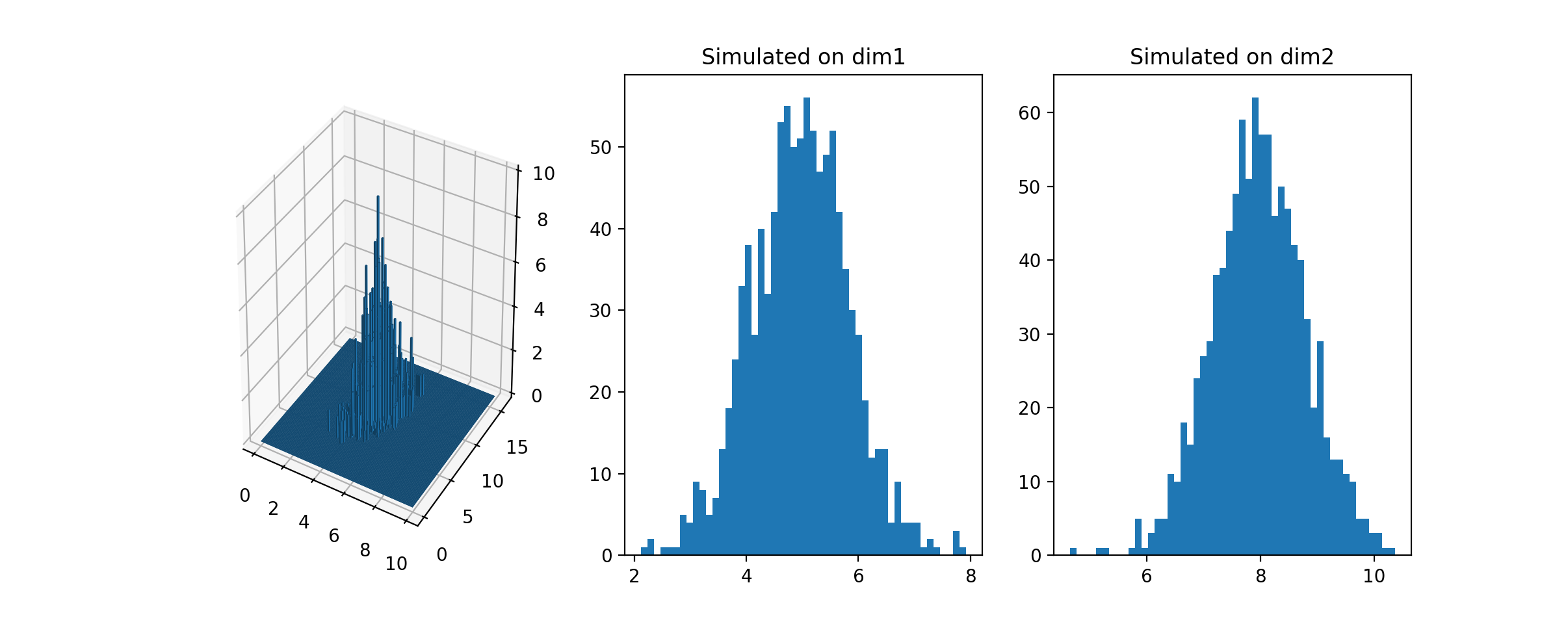
来看个例子吧。假设我们有二维正态分布:

\[\begin{align} \mu &=(\mu1,\mu2)\\ \\ \Sigma &=\begin{pmatrix} \sigma_1^2 & \rho\sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{pmatrix} \\ \\ P(x_1|x_2) &= Norm(\mu_1+\rho\sigma_1/\sigma_2(x_2-\mu_2), (1-\rho^2)\sigma_1^2) \\ \\ P(x_2|x_1) &= Norm((\mu_2+\rho\sigma_2/\sigma_1(x_1-\mu_1), (1-\rho^2)\sigma_2^2) \end{align}\]

假设我们期望抽样的二元正态分布是 $\mu=(5,8)$, 协方差矩阵为 \(\begin{pmatrix} 1& 0.5 \\ 0.5 & 1 \end{pmatrix}\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
 
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np


class Transition():
    def __init__(self, mean, cov):
        self.mean = mean
        self.sigmas = []
        for i in range(K):
            self.sigmas.append(np.sqrt(cov[i][i]))
        self.rho = cov[0][1]/(self.sigmas[0] * self.sigmas[1])

    def sample(self, id1, id2_list, x2_list):
        id2 = id2_list[0]  # only consider two dimension
        x2 = x2_list[0]  # only consider two dimension
        cur_mean = self.mean[id1] + self.rho*self.sigmas[id1]/self.sigmas[id2] * (x2-self.mean[id2])
        cur_sigma = (1-self.rho**2) * self.sigmas[id1]**2
        return np.random.normal(cur_mean, scale=cur_sigma, size=1)[0]


def gibbs(p, m, n):
    # randomize a number
    x = np.random.rand(K)
    for t in range(0, m+n):
        for j in range(K):
            total_indexes = list(range(K))
            total_indexes.remove(j)
            left_x = x[total_indexes]
            x[j] = p.sample(j, total_indexes, left_x)

        if t >= m:
            yield x


mean = [5, 8]
cov = [[1, 0.5], [0.5, 1]]
K = len(mean)
q = Transition(mean, cov)
m = 100
n = 1000

gib = gibbs(q, m, n)

simulated_samples = []

x_samples = []
y_samples = []
for li in gib:
    x_samples.append(li[0])
    y_samples.append(li[1])


fig = plt.figure()
ax = fig.add_subplot(131, projection='3d')

hist, xedges, yedges = np.histogram2d(x_samples, y_samples, bins=100, range=[[0,10],[0,16]])
xpos, ypos = np.meshgrid(xedges[:-1], yedges[:-1])
xpos = xpos.ravel()
ypos = ypos.ravel()
zpos = 0

dx = xedges[1] - xedges[0]
dy = yedges[1] - yedges[0]
dz = hist.flatten()

ax.bar3d(xpos, ypos, zpos, dx, dy, dz, zsort='average')

ax = fig.add_subplot(132)
ax.hist(x_samples, bins=50)
ax.set_title("Simulated on dim1")

ax = fig.add_subplot(133)
ax.hist(y_samples, bins=50)
ax.set_title("Simulated on dim2")
plt.show()

代码运行结果: gibbs_simulation

Tricks

从马尔科夫链蒙特卡洛法中我们得到的样本序列，相邻点是相关的，因此如果需要独立样本，我们可以在该样本序列中再次进行随机抽样，比如每隔一段时间抽取一次样本，将这样得到的样本集合作为独立样本集合。

另外，关于“燃烧期”,即过多少步后马尔科夫链是趋向稳定分布的，通常是经验性的。比如书上说，可以游走一段时间后采集的样本均值和过一段时间后采集的样本均值做个比较，如果均值稳定，那可以认为马尔科夫链收敛。

总结

本文回顾了马尔科夫链蒙特卡洛法的相关基本知识点、Metropolis-Hastings, Gibbs sampling基本原理。下一篇文章，我们一起来看看MCMC大法在实际应用中的一些例子。

Reference

[1] 李航. 统计学习方法第二版[J]. 2019.

[2] https://www.cnblogs.com/pinard/p/6625739.html