基础概念
指示函数
指示函数(Indicator Function)通常写成 $I_{{A}}(x)$ ,有的时候也写成 $\mathds{1}{{A}}(x)$, 也有时候写成 $I{{A}}$。例子:
\[I_{\{x>3\}}=\left\{ \begin{aligned} 0 && x\leq3\\ 1 && x \gt 3 \end{aligned} \right.\]期望
期望或者均值常常写作 $E(X)$, 它是随机变量 $X$ 可以取的值的加权平均值,权重取决于这些值的概率。 假设 $X$ 是离散值,那么有:
\[E(X) = \sum_x x \cdot P(X=x) = \sum_x x \cdot f(x)\]如果 $X$ 是连续随机变量,概率密度函数(probability density function, PDF)为 $f(x)$, 我们把求和符号换成积分:
\[E(X) = \int_{-\infty}^{+ \infty} x \cdot f(x) dx\]我们也可以计算 $X$ 的函数的期望, 比如: 假设 $g(X) = \frac 2X$, 那么我们又 $E(g(X))=\int_{-\infty}^{+ \infty}g(x)f(x)dx =\int_{-\infty}^{+ \infty}\frac 2x f(x) $
方差
方差用来衡量随机变量的值有多分散,如果 $X$ 是一个随机变量,它的均值$E(X) = \mu$,那么它的方差为 $E[(X-\mu)^2]$。如果 $X$ 是离散的,那么:
\[Var(X) = \sum_x (x-\mu)^2 \cdot P(X=x)\]如果 $X$ 是连续值,那么:
\[Var(X) = \int_{- \infty}^{\infty} (x-\mu)^2 \cdot f(x) dx\]一个计算方差比较方便的公式是: $Var(X) = E[X^2] - (E[X])^2$。方差的平方根叫做标准差。
假设 $Var(X) = \sigma_X^2$,$Var(Y) = \sigma_Y^2$, 并且$X$和$Y$是独立的,一个新的随机变量 $Z= aX + bY + c$,其中 $a,b,c$ 都是实数常量。 那么:
\[Var(Z) = Var(aX + bY + c) = a^2Var(X) + b^2Var(Y) + 0 = a^2\sigma_X^2 + b^2\sigma_Y^2\]因为 $c$ 是常量,所以方差为 $0$。
极大似然估计
似然(likelihood)函数是参数 $\theta$ 的函数,其中数据 $y$ 是固定的。因此当我们对 log-likelihood 函数求导,其实是对 $\theta$ 求导。对参数求导后,令式子等于0,解得参数的极大似然估计。
这里记录几个分布的极大似然估计(MLE, maximum likelihood estimate):
| Distribution | MLE |
|---|---|
| $N(\mu, \sigma^2)$ | $\hat{\mu} = \frac{1}{n}\sum_{i=1}^ny_i = \bar{y} \quad \hat{\sigma^2} = \frac{1}{n}\sum_{i=1}^n (y_i-\hat{\mu})^2$ |
| Bernoulli | $\hat{p} = \frac{1}{n}\sum_{i=1}^ny_i = \bar{y}$ |
| $Exp(\lambda)$ | $\frac{1}{\hat{\lambda}}= \frac{1}{n}\sum_{i=1}^ny_i = \bar{y}$ |
共轭
共轭是个很好的性质,它可以使得我们的后验概率表达式变得更容易计算(不用计算分母的积分)。(很多实际例子都是没有这个性质的,所以通常会用采样的方式,像是 MCMC)。 共轭的指的是当后验分布和先验分布在一个概率密度函数家族中,而后验分布可能更新了参数则可以理解为它从实际的数据中学习到了一些信息。这里罗列几个共轭家族。
| Prior | Likelihood | Posterior |
|---|---|---|
| $p \sim Beta(\alpha, \beta)$ | $x \sim Bin(n,p)$ | $Beta(\alpha + x, \beta + n - x)$ |
| $\lambda \sim Gamma(\alpha, \beta)$ | $Y_i \sim Pois(\lambda)$ | $Gamma(\alpha + \sum y_i, \beta + n)$ |
| $\lambda \sim Gamma(\alpha, \beta)$ | $Y_i \sim Exp(\lambda)$ | $ Gamma(\alpha + n, \beta + \sum_yi)$ |
| $\mu \sim N(m_0, s_0^2)$ | $X_i \overset{\text{iid}}{\sim} N(\mu, \lambda_0^2)$ $\lambda$ is known $ | $N(\frac{n\bar{x}s_0^2 + m_0\sigma_0^2}{ns_0^2 + \sigma_0^2}, \frac{s_0^2\sigma_0^2}{ns_0^2+\sigma_0^2})$ |
| $\mu |\sigma^2 \sim N(m, \frac{\sigma^2}{w}) \quad \sigma^2 \sim \Gamma^{-1}(\alpha, \beta)$ | $X_i \overset{\text{iid}}{\sim} N(\mu, \lambda_0^2)$ | $\sigma^2 |x \sim \Gamma^{-1}(\alpha+\frac n2, \beta + \frac 12\sum_{i=1}^n(x_i - \bar{x})^2 + \frac{nw}{2(n+w)}(\bar{x}-m)^2)$ $\mu |\sigma^2, x \sim N(\frac{n\bar{x} + wm}{n+w}, \frac{\sigma^2}{n+w}) \quad w=\frac{\sigma^2}{\sigma_\mu^2}$ |
置信区间和可信区间
置信区间(confidence interval) 频率学派专用。 可信区间(credible interval) 贝叶斯统计专用。
举个例子:
95% confidence interval on the mean is that “95% of similarly constructed intervals will contain the true mean” 对于频率学家来说,一个随机变量只能存在两种状态,要么在这个区间,要不在这个区间,所以不可以说成是在95%的概率在这个区间,而应该说成是95%类似的区间包含了真正的均值。
95% credible interval on the mean is that “the probability that the true mean is contained within a given interval is 0.95” 对于贝叶斯学派就不存在这个问题了。
常见的分布
一般对于离散值的概率分布称为: PMF(Probability Mass Function), 连续值的概率分布称为: 概率密度函数- PDF(Probability Density Function)。连续值的概率分布是针对一个区间的。
常见的离散值概率分布
伯努利分布
伯努利分布(Bernoulli distribution), 又名两点分布或0-1分布。如果伯努利实验成功,离散随机变量值为1,否则为0。假设成功的概率 $p$, 那么它的概率质量函数为:
\[f_X(x)= p^x(1-p)^{1-x} = \left\{ \begin{aligned} p && x=1\\ 1-p && x=0 \end{aligned} \right.\]期望$E[X] = p$, 方差$Var[X]=p(1-p)$
二项式分布
二项式分布(Binonmial distribution)是伯努利分布的更一般的形式。设随机变量 $X$ 为 $n$ 重贝努力实验中成功的次数,那么 $X$的取值可能为 $0,1, \dots, n$,它取这些 值的概率为:
\[P(X=x) = \left(\begin{matrix} n \\ x\end{matrix} \right) p^x(1-p)^{n-x}, \quad x=0,1, \dots, n\]其中 $\left(\begin{matrix} n \ x\end{matrix} \right) = \frac{n!}{x!(n-x)!}$ 为二项式系数
记作 $X \sim b(n,p)$, 当 $n=1$ 时,变为伯努利分布。
期望$E[X]=np$, 方差$Var[X]=np(1-p)$
几何分布
几何分布(Geometric distribution),指的是第一次出现成功所需要的次数,比如贝努力实验中,第一次掷硬币掷出正面需要的实验次数。
\[\begin{align} X &\sim Geo(p)\\ P(X=x|p) &=p(1-p)^{x-1} \quad x=1,2,\dots \\ \end{align}\]期望$E[X]=\frac 1p$, 方差 $Var[X] = \frac{1-p}{p^2}$
多项式分布
多项式分布(Multinomial distribution),是伯努利分布和二项式分布的更一般形式。类似于二项式分布,但是结果不单单是只有两种(成功或失败),它有更多的结果。假设 $n$ 次实验,有 $k$ 种可能的结果 $p_1, \dots, p_k$。举个例子,一个六个面的骰子,每个面出现的概率分别为$p_1, \dots, p_6$, 在$n$次掷骰子中,每个面出现的次数分别为 $x_1, \dots, x_6$,那么 $\sum_{i=1}^6 x_i=n$,$\sum_{i=1}^6 p_i=1$。
\[f(x_1, \dots, x_k | p_1, \dots, p_k) = \frac{n!}{x_1!\dots x_k!}p_1^{x_1}\dots p_k^{x_k}\]每个类$i$ 的期望是 $np_i$
泊松分布
泊松分布(Poisson distribution)经常用于计数,参数 $\lambda \gt 0$。泊松分布中事件的平均发生频率为 $\lambda$,事件之间是独立的。
\[\begin{align} X &\sim Pois(\lambda)\\ P(X=x|\lambda) &=\frac{\lambda^x \exp(-\lambda)}{x!} \quad x=1,2,\dots \\ E[X] &= \lambda \\ Var[X] &= \lambda \end{align}\]常见的连续值概率分布
指数分布
指数分布通常用于建模随机事件之间的等待时间。如果在连续的事件之间的等待时间独立且服从指数分布 $Exp(\lambda)$, 那么对于任意的固定时间长度为 $t$ 的窗口,发生在那个窗口中的事件次数就会服从一个泊松分布,均值为 $t\lambda$
\[\begin{align} X &\sim Exp(\lambda)\\ P(X=x|\lambda) &= \lambda e^{-\lambda x} I_{\{ x \ge 0 \}(x)} \\ E[X] &= \frac 1\lambda \\ Var[X] &= \frac 1\lambda^2 \end{align}\]类似于泊松分布, 参数 $\lambda$ 也可以解释为事件发生的频率。
伽马分布
如果$X_1, X_2, \dots, X_n$ 是独立的 (并且都服从指数分布 $Exp(\lambda)$)的连续事件之间的等待时间,那么为了让所有$n$ 个事件都发生的总的等待时间 $Y=\sum_{i=1}^n X_i$ 遵循一个伽马分布(Gamma distribution),它的形状参数 $\alpha=n$,频率(尺度)参数 $\beta = \lambda$。
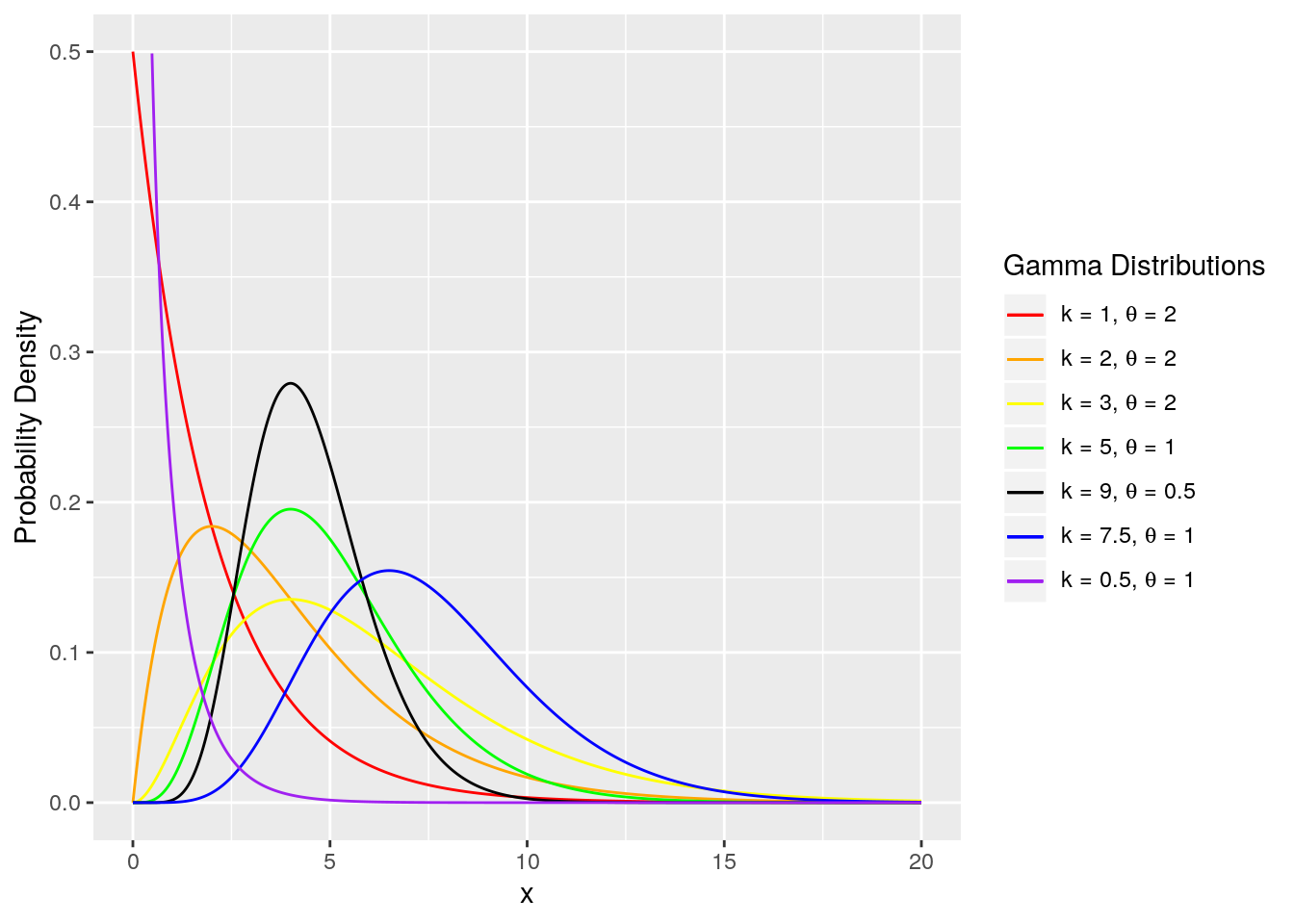
\[\begin{align} Y &\sim Gamma(\alpha, \beta)\\ f(y|\alpha, \beta) &= \frac{\beta^\alpha}{\Gamma(\alpha)}y^{\alpha-1}e^{-\beta y} I_{\{ y \ge0\}}(y) \\ E[X] &= \frac{\alpha}{\beta}\\ Var[X] &= \frac{\alpha}{\beta^2} \end{align}\]其中, $\Gamma(\cdot)$ 为伽马函数,阶乘函数的一般式。比如 $n$ 为一个正整数,$\Gamma(n) = (n-1)!$。注意 $\alpha > 0$, $\beta > 0$。 指数分布是 $\alpha=1$ 的伽马分布的一个特例。当 $\alpha$ 增大,伽马分布就会更加像正态分布。$E[X]= \frac{\alpha}{\beta}$,方差 $Var[X] = \alpha / \beta^2$。图来自[2] (图中用 $k$ 和 $\theta$ 来表示 $\alpha$ 和 $\frac 1\beta$)。
均匀分布
均匀分布(Uniform distribution),是随机变量取值在一个范围区间内都是同等概率的。假设区间为 $(a,b)$,那么均匀分布概率密度函数$f(x)$在这个区间内值是一样的,在区间外都为 $0$.
\[\begin{align} X &\sim Uniform(a, b)\\ f(x|a, b) &= \frac{1}{b-a}I_{\{ a \le x \le b\}}(x) \\ E[X] &= \frac{a+b}{2}\\ Var[X] &= \frac{(b-a)^2}{12} \end{align}\]贝塔分布
贝塔分布(Beta distribution)专门用在取值为0到1之间的随机变量上。因为这个原因(以及其他的一些原因),贝塔分布经常用于建模概率。
\[\begin{align} Y &\sim Beta(\alpha, \beta)\\ f(x|\alpha, \beta) &= \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} I_{\{ 0 < x < 1\}}(x) \\ E[X] &= \frac{\alpha}{\alpha+\beta}\\ Var[X] &= \frac{\alpha \beta}{(\alpha+\beta)^2(\alpha+\beta+1)} \end{align}\]其中, $\Gamma(\cdot)$ 为伽马函数。 注意 $\alpha > 0$, $\beta > 0$。标准均匀分布 $Uniform(0,1)$ 是贝塔分布的一个特例,其中$\alpha=\beta=1$。
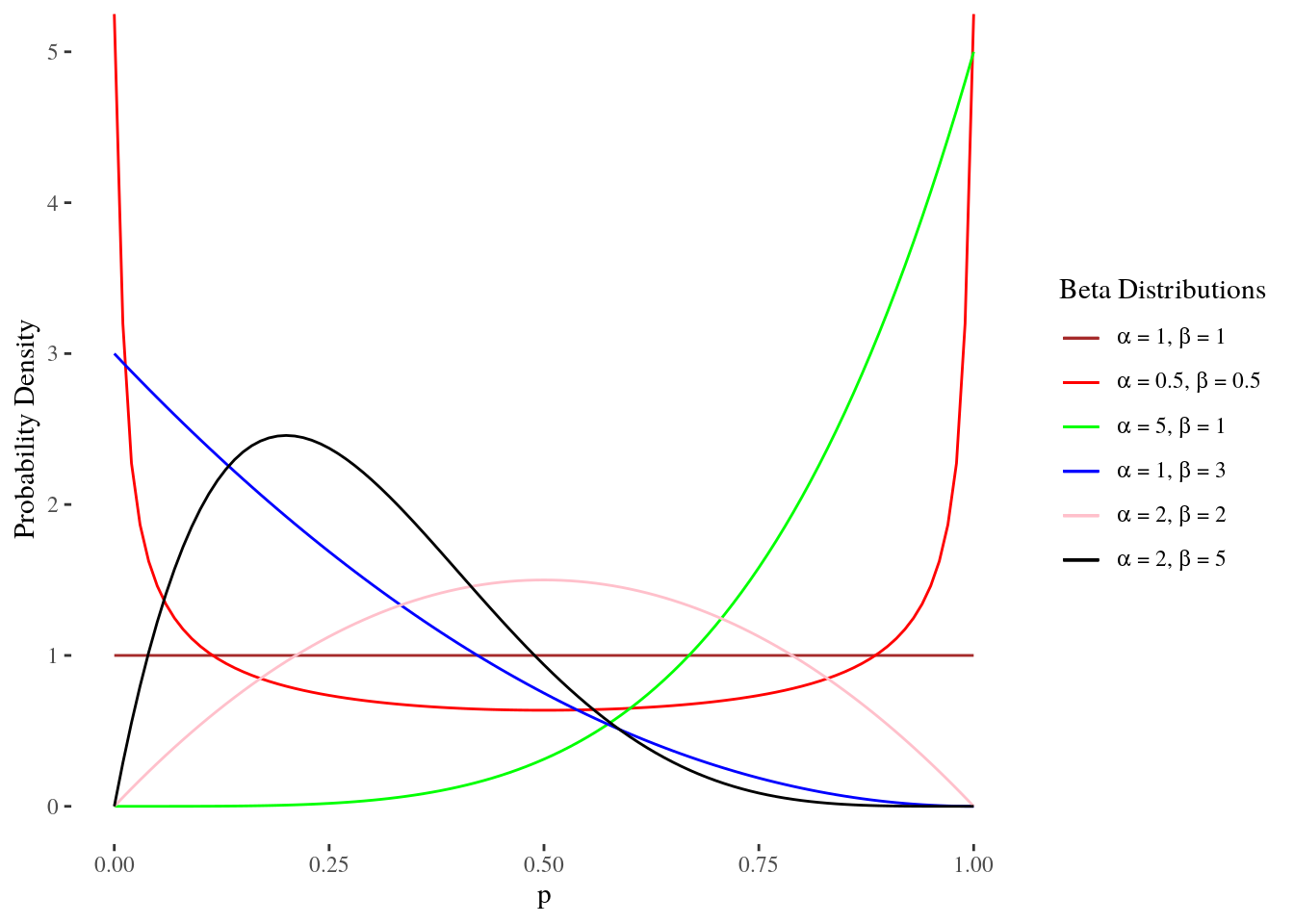
期望$E[X]=\frac{\alpha}{\alpha+\beta}$。举个简单的例子,在一系列的实验中,硬币朝上的次数计作 $\alpha$, 硬币朝下的次数计作 $\beta$, 那么概率 $X$ 的期望值为 $E[X]=\frac{\alpha}{\alpha+\beta}$ 。方差 $Var[X] = \frac{\alpha\beta}{(\alpha + \beta)^2(\alpha+\beta+1)}$ 图来自[2]。
正态分布
正态分布 (Normal distribution), 或者高斯分布,经常用来建模 “errors”,或者回归模型中的每个样本的波动(unexplained variation)。
\[\begin{align} Y &\sim N(\mu, \sigma^2)\\ f(x|\mu, \sigma) &= \frac{1}{\sqrt{2\pi \sigma^2}}\exp(-\frac{(x-\mu)^2}{2\sigma^2}) \end{align}\]正态分布有一些很好的特性。如果 $X_1 \sim N(\mu_1, \sigma_1^2)$, $X_2 \sim N(\mu_2, \sigma_2^2)$ 互相独立,那么 $X_1 + X_2 \sim N(\mu_1 + \mu_2, \sigma_1^2 + \sigma_2^2)$。因此,如果我们假设有 $n$ 个独立同分布(independent and identically distributed, iid)的正态随机变量:
$\bar{X} = \frac 1n \sum_{i=1}^n X_i$
其中, $X_i \overset{\text{iid}}{\sim} N(\mu, \sigma^2), i=1,2,\dots, n$, 那么:
$\bar{X} \sim N(\mu, \frac{\sigma^2}{n})$
t分布
当我们有了正态分布数据,我们可以通过逆转上一节的式子来帮我们评估均值 $\mu$,得到:
$\frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim N(0,1)$
但是我们不知道 $sigma$ 的值,如果我们用数据样本来评估它,用 $ S= \sqrt{\sum_i(X_i - X)^2/(n-1)}$ (样本标准差)来代替它,这会导致上面的表达式不再是标准的正态分布,但它会是一个标准的 $t$ 分布, 自由度为 $v=n-1$
\[\begin{align} Y &\sim t_v\\ f(x) &= \frac{\Gamma(\frac{v+1}{2})}{\Gamma(\frac v2)\sqrt{v \pi}}\left(1+\frac{y^2}{v}\right)^{-(\frac{v+1}2)} \\\\ E(Y) &= 0, if v>1 \\\\ Var(Y) &= \frac{v}{v-2}, if v>2 \end{align}\]t分布和正态分布很想,只是尾部更加宽,随着自由度的增加,t分布会越来越像标准正态分布。
常见的定理
中心极限定理
中心极限定理 (Central Limit Theorem), 大体上的意思是随着样本数量的增加,样本均值服从一个正态分布。假设 $X_1, \dots, X_n$ 是独立同分布的,其中 $E[X_i] = \mu$, $Var(X_i)=\sigma^2$, 那么:
\[\frac{\sqrt{n}(\bar{X}-\mu)}{\sigma} \Rightarrow N(0,1)\]$\bar{X}_n$ 近似正态分布,均值为 $\mu$,方差 $\sigma^2/n$
连续随机变量分布的贝叶斯定理
\[f(\theta|y) = \frac{f(y|\theta)f(\theta)}{\int f(y|\theta)f(\theta) d\theta}\]参考
[1] https://coursera.org/learn/bayesian-statistics
[2] https://statswithr.github.io/book/bayesian-inference.html